哈夫曼编码是一种在无损信息的情况下压缩数据的有效方法。在计算机科学中,信息被编码为比特:1 和 0。位串编码的信息告诉计算机要执行哪些指令。视频游戏、照片、电影等等在计算机中被编码为比特串。计算机每秒执行数十亿条指令,而一个视频游戏可能是数十亿比特的数据。不难看出,为什么高效和不含糊的信息编码是计算机科学中一个令人感兴趣的话题。
哈夫曼编码通过分析某些符号在信息中出现的频率,提供了一种高效、明确的编码。出现频率较高的符号将被编码为较短的比特串,而使用频率不高的符号将被编码为较长的字符串。然后用这种频率的编码来替换原来的信息,出现频率较高的就会替换为较短的编码,从而节省空间。
举个例子:
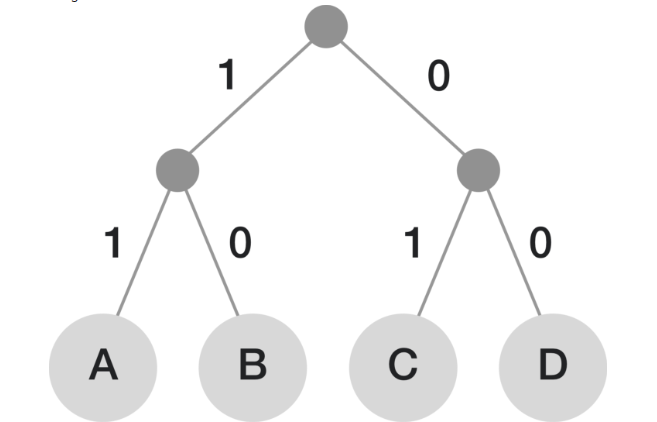
上面图中对字符串ABCD构建一个 huffman 的二叉树,如果要对 CBA 编码,结果就是011011.
由于符号的频率在不同的信息中是不同的,所以没有一种哈夫曼编码可以适用于所有的信息。这意味着,发送消息 X 的哈夫曼编码可能与发送消息 Y 的哈夫曼编码不同。
huffman 的原理
对于哈夫曼编码的原理,我是看了这个教程就了解了,我直接搬运过来,借鉴下大佬的讲解。重点的地方,我自己第一次没有太理解的地方,我加了部分补充来理解。
下面是we will we will r u中每个字符出现的频率。

构建二叉树
对于上面这样的值,构建一个二叉树来表达每一个字符的路径信息。
初始队列
那么我们按出现频率高低将其放入一个优先级队列中,从左到右依次为频率逐渐增加。

下面我们需要将这个队列转换成哈夫曼二叉树,哈夫曼二叉树是一颗带权重的二叉树,权重是由队列中每个字符出现的次数所决定的。并且哈夫曼二叉树始终保证权重越大的字符出现在越高的地方。这样就是出现频率越高的字符,编码的路径就越短,这样编码出来的结果就越少。
第一步合并
首先我们从左到右进行合并,依次构建二叉树。第一步取前两个字符 u 和 r 来构造初始二叉树,第一个字符作为左节点,第二个元素作为右节点,然后两个元素相加作为新空元素,并且两者权重相加作为新元素的权重。
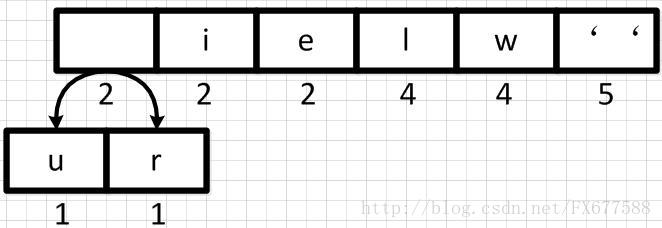
同理,新元素可以和字符 i 再合并,如下:
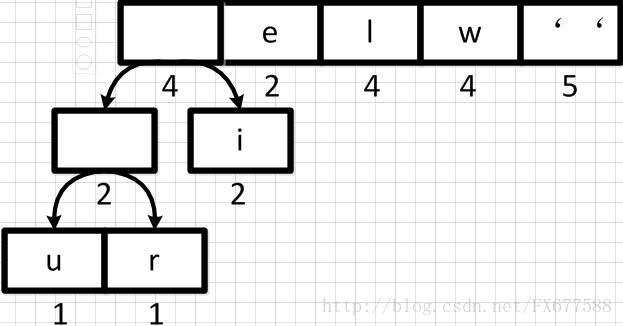
重新调整队列
上图新元素权重相加后结果是变大了,需要对权重进行重新排序。
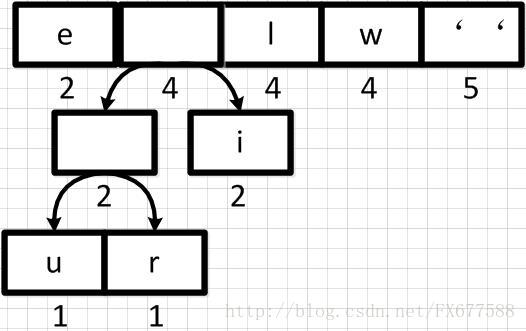
然后再依次从左到右合并,每合并一次则进行一次队列重新排序调整。如下:
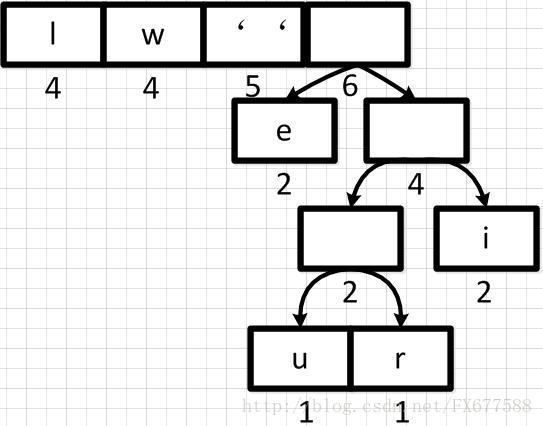
经过多步操作之后,得到以下的哈夫曼二叉树结构,也就是一个带有权重的二叉树:
重点就是当根节点的权重大于剩余权重的时候,就要新开一个节点,下图中的I、W,权重都是4,而当前根节点的权重为11,所以就新开了一个节点。
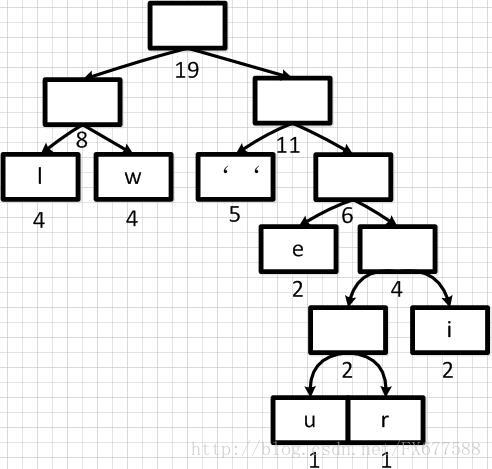
哈夫曼编码
有了上面带权重的二叉树之后,我们就可以进行编码了。我们把二叉树分支中左边的支路编码为 0,右边分支表示为 1,如下图:
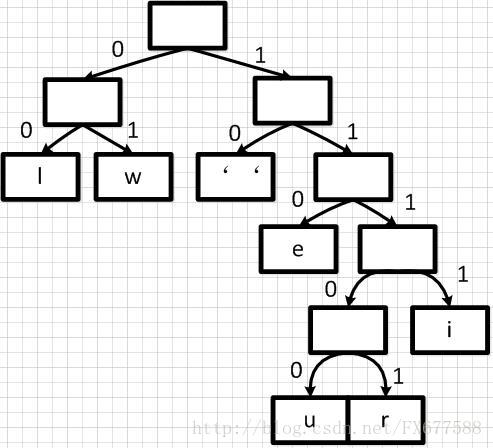
这样依次遍历这颗二叉树就可以获取得到所有字符的编码了。例如:‘ ’的编码为 10,‘l’的编码为 00,‘u’的编码为 11100 等等。经过这个编码设置之后我们可以发现,出现频率越高的字符越会在上层,这样它的编码越短;出现频率越低的字符越会在下层,编码越短。经过这样的设计,最终整个文本存储空间才会最大化的缩减。 最终我们可以得到下面这张编码表:

show me the code
huffman 的具体实现步骤: 1)将信源符号的概率按减小的顺序排队。 2)把两个最小的概率相加,并继续这一步骤,始终将较高的概率分支放在右边,直到最后变成概率 1。 3)画出由概率 1 处到每个信源符号的路径,顺序记下沿路径的 0 和 1,所得就是该符号的霍夫曼码字。 4)将每对组合的左边一个指定为 0,右边一个指定为 1(或相反)。
// 这是一个关于 Huffman 编码的测试用例
#include <iostream>
#include <queue>
#include <vector>
#include <string>
#include <unordered_map>
using namespace std;
// Huffman 树节点
struct Node {
char ch;
int freq;
Node* left;
Node* right;
Node(char c, int f) : ch(c), freq(f), left(nullptr), right(nullptr) {}
~Node() {
delete left;
delete right;
}
};
// 比较函数,用于优先队列
struct cmp {
bool operator()(Node* a, Node* b) {
return a->freq > b->freq;
}
};
// 构建 Huffman 树
Node* buildHuffmanTree(unordered_map<char, int>& freq) {
priority_queue<Node*, vector<Node*>, cmp> pq;
for (auto& p : freq) {
pq.push(new Node(p.first, p.second));
}
while (pq.size() > 1) {
Node* left = pq.top();
pq.pop();
Node* right = pq.top();
pq.pop();
Node* parent = new Node('$', left->freq + right->freq);
parent->left = left;
parent->right = right;
pq.push(parent);
}
return pq.top();
}
// 递归函数,用于生成 Huffman 编码
void generateHuffmanCode(Node* root, string code, unordered_map<char, string>& huffmanCode) {
if (!root) {
return;
}
if (root->ch != '$') {
huffmanCode[root->ch] = code;
}
generateHuffmanCode(root->left, code + "0", huffmanCode);
generateHuffmanCode(root->right, code + "1", huffmanCode);
}
// 打印 Huffman 编码
void printHuffmanCode(unordered_map<char, string>& huffmanCode) {
for (auto& p : huffmanCode) {
cout << p.first << " " << p.second << endl;
}
}
int main() {
string str = "hello world";
unordered_map<char, int> freq;
for(decltype(str.size()) i = 0; i < str.size(); ++i) {
++freq[str[i]];
}
Node* root = buildHuffmanTree(freq);
unordered_map<char, string> huffmanCode;
generateHuffmanCode(root, "", huffmanCode);
printHuffmanCode(huffmanCode);
delete root;
return 0;
}
输出的结果:
# 打印的huffman编码结果
w 1111
h 001
o 01
e 000
l 10
r 1100
1110
d 1101
对应的hello world的编码就是如下
for (char c : str) { // iterate over each character in the string
// std::cout << c << std::endl; // print the character
cout << huffmanCode[c] ;
}
// 00100010100111101111011100101101
最后的长度就是 32 位,如果用原始的编码是实现,就是 11*8=88 位才能存下,空间减少 63%,可见这个效果是多么的好。
更多阅读
微信公众号:cdtfug,欢迎关注一起吹牛逼,也可以加微信号「xiaorik」朋友圈围观。